4 雙產品市場

4.1 價量關係

Given products $j \in \left \{ 1,2 \right \}$, prices $p_j$, costs $c_j$, and respondent $i$’s utilities $u_{i,j}$ :

\[ \begin{cases} q_j(p_j,p_{j'}) = \sum_i I(u_{i,j} > p_j \text{ and } u_{i,j} - p_j > u_{i,j'} - p_{j'} ) & \text{; quantity} \\ \\ r_j(p_j,p_{j'}) = q_j(p_j,p_{j'}) * p_j & \text{; revenue} \\ \\ \pi_j(p_j,p_{j'}) = q_j(p_j,p_{j'}) * (p_j - c_j) & \text{; profit} \end{cases} \]
如果市場上有兩項產品 $j$ and $j'$，消費者 $i$ 會購買產品 $j$ 需要同時滿足兩個條件：

買 $j$ 的剩餘大於 $0$： $u_{i,j} - p_j > 0$
買 $j$ 的剩餘大於買 $j'$ 的剩餘： $u_{i,j} - p_j > u_{i,j'} - p_{j'}$

依照上面的公式，我們可以做出雙產品市場的儀表板：

p1 = seq(4.5,10.5,0.1); p2 = seq(4.5,10.5,0.1)
pd1 = c(1,1,3,1); pd2 = c(3,2,3,1)
nm = 
mc1 = PC(pd1); mc2 = PC(pd2)
u1 = UT(pd1); u2 = UT(pd2)
x1 = 7.9; x2 = 6.5
s1 = u1 - x1; s2 = u2 -x2
dcs = rep(4, nrow(W))
dcs[s1 > 0 & s1 > s2] = 1
dcs[s2 > 0 & s2 > s1] = 2
dcs[s1 > 0 & s1 == s2] = 3
clr = c('magenta','blue','gold','gray')

Profit = function (id, p, px, m, u, s2, nm, flag=F) {
  q = sapply(p, function(x) sum(u > x & u - x > s2) )
  pf = (p-m)*q
  pst = p[which.max(pf)]
  qx = sum(u > px & u - px > s2) + 0.5*sum(u > px & u - px == s2)
  rx = qx * px
  pfx = qx * (px-m)
  par(cex=0.7,mar=c(3,3,3,2))
  st = ifelse(id == 1, "$\\pi_1(p_1|p_2)", "$\\pi_2(p_2|p_1)")
  plot(p, pf, type='l',ylab="",ylim=c(0,100),xlab="",
       main=sprintf("PD: %s\nProfit = %.1f @ %.1f (mc=%.1f)",
                    nm[id],pfx,px,m),
       col.main=clr[id], cex.axis=0.8, cex.main=1)
  abline(v=px,col=clr[id])
  abline(v=pst,col='green',lty=3,lwd=2)
  abline(h=c(20,40,60,80),col='lightgray',lty=2)
  text(max(p)-0.5, 103,TeX(sprintf("%.1f^*",pst)),pos=1,col='green',cex=1.1)
  text(min(p)+0.8, 103, TeX(st) ,pos=1,cex=1.2)
  if(flag) points(max(p)-0.6, 100, pch=19, col='green')
  return( c(pfx,rx,pst) )
}

layout(matrix(c(1,2,3,4,4,5),3,2,byrow=F),
       widths=c(0.9,1.2),heights=c(1,1,1.2))
nm = sapply(list(pd1,pd2),paste0, collapse="")
f1 = Profit(1, p1, x1, mc1, u1, s2, nm)
f2 = Profit(2, p2, x2, mc2, u2, s1, nm)

pene = 100 * sum(dcs!=4)/nrow(W)
tpro = sum(dcs==1)*(x1 - mc1) + sum(dcs==2)*(x2 - mc2)
trev = sum(dcs==1)*x1 + sum(dcs==2)*x2
tb = table(dcs)
par(mar=c(3,3,4,3))
pie(tb,paste0(as.character(tb),'%'),col=clr[as.integer(names(tb))],
    main=sprintf("Panetration = %.1f%%",pene),
    cex.main=1.1,font=2,cex=1,border='white')

par(mar=c(5,4,5,2))
plot(u1,u2,pch=20,col=clr[dcs],cex=2,cex.lab=1.2,
  xlab=TeX("$U_1$"),ylab=TeX("$U_2$"),
  main=sprintf("\n\nUtility Space\nTotal Revenue (%.1f) & Profit (%.1f)",
               trev,tpro),cex.main=1.1)
abline(v=x1,col=clr[1]);abline(h=x2,col=clr[2])
lines(x=c(x1,x1+10),y=c(x2,x2+10),col='gray',lty=3,lwd=2)

par(mar=c(3,4,3,2),cex=0.7)
bp = cbind(c(f1[1],f1[2]-f1[1],0,0),c(0,0,f2[1],f2[2]-f2[1]))
barplot(bp,names=c('prod-1','prod-2'),main="Revenue & Profit (Margin)",
        ylim=c(0,280),col=c(clr[1],'pink',clr[2],'cyan'),
        cex.main=1.1,border=NA )
abline(h=seq(50,250,50),lty=3,col='gray')
for(t in list(c(0.7,f1[1],f1[1]),c(0.7,f1[2],f1[2]),
              c(1.9,f2[1],f2[1]),c(1.9,f2[2],f2[2]) ) )
  text(t[1],t[2]-10,t[3],font=2,pos=3)
text(0.7,250,sprintf("(%.1f%%)",100*f1[1]/f1[2]),font=2,pos=3)
text(1.9,250,sprintf("(%.1f%%)",100*f2[1]/f2[2]),font=2,pos=3)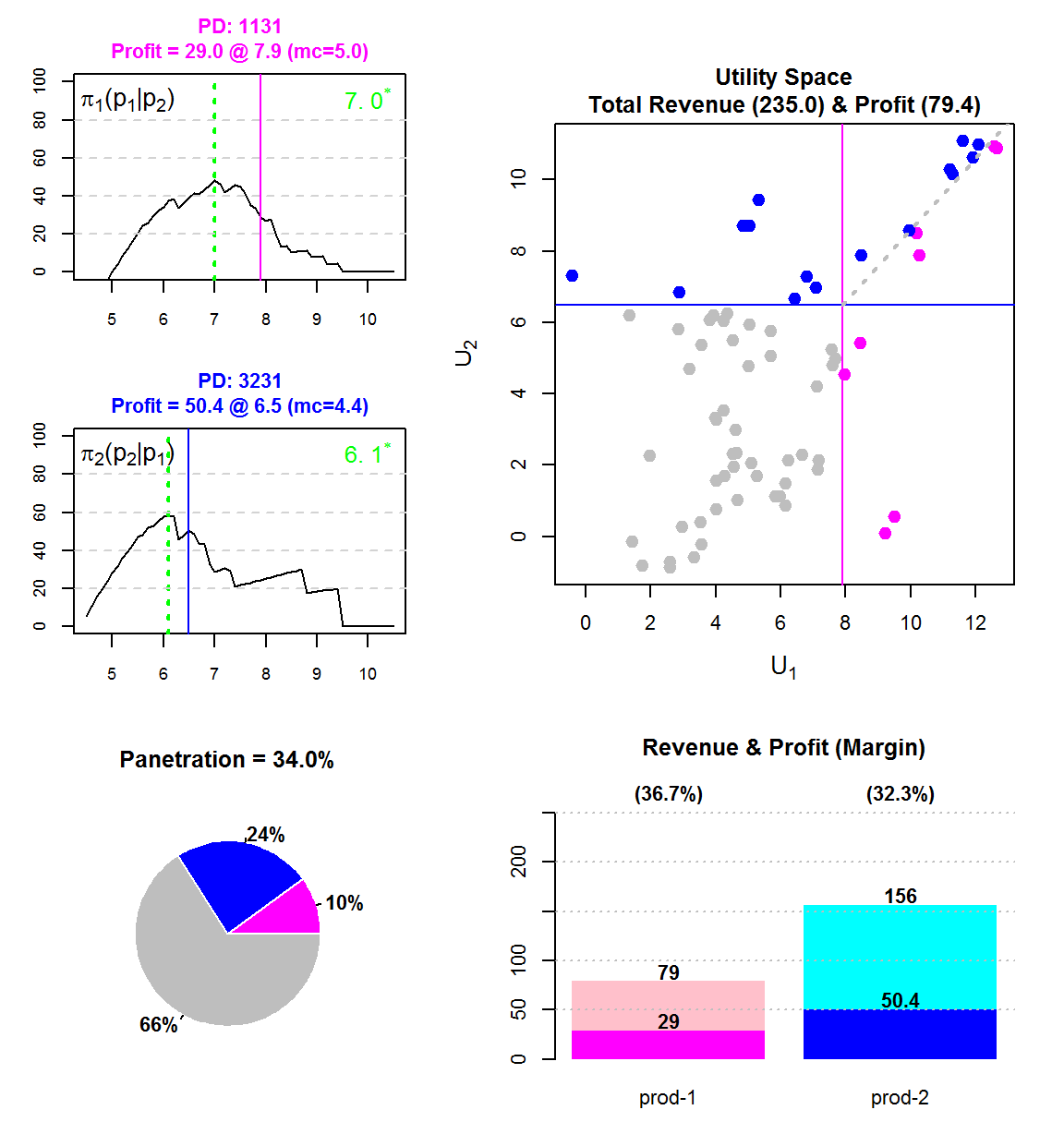

SIM-3: 雙產品市場模擬

source("sim3.R")

4.2 競爭策略

假如市場上有一個競爭產品 PD1=c(1,1,3,1)，它的價格設在$7.5 :

如果我們推出相同的產品，價格設在 $7.0，結果是？
如果我們把價格升高到$7.4，結果會比較好嗎？
如果我們賣$7.4，對手會如何回應呢？
這個賽局最後的結果會是如何？
如果兩個廠商的邊際成本不一樣，結果會是如何？
這段練習有哪些的策略意涵？

假如市場上有兩個競爭產品 PD1=c(3,3,3,2) & PD2=c(1,3,3,2) :

均衡時雙方的營收和獲利是？
假如你是PD1，在均衡的狀況之下你會想要調整價格嗎？你會調到什麼價格呢？
假如你是PD2，你會如何回應PD1的價格調整呢？
如果雙方的策略目標都是利潤最大化，結果是如何？
如果PD1策略目標是市占率最大化，結果會一樣嗎？
想看看，這段練習的策略意涵是什麼？

最後我們做一個開放性的練習，假如市場上已有一個競爭產品 PD1=c(3,3,3,2) @ $7.5 :

你要用什麼產品和價格進入市場？為什麼？

4.3 產品線規劃

假如你要在一個新市場(沒有競爭產品)裡面，規劃一條有兩個產品的產品線：

你的策略目標是什麼？
你的產品規格、價格？營收、獲利、滲透率？
你確定這是達成你的策略目標最好的策略嗎？你如何才能確定？

4.4 自動模擬

4.4.1 價格空間

像新產品設計一樣，我們也可用自動模擬程式幫助我們規劃產品線。但是雙產品的市場比較複雜，兩個產品會有兩個價格，我們首先要確定：

兩產品互相競爭時的均衡價格
兩產品合作時的最佳價格

### 4.2
pSpace = function(pd1, p1, pd2, p2) {
  mc1 = PC(pd1); mc2 = PC(pd2)
  u1 = UT(pd1); u2 = UT(pd2)
  q1 = q2 = f0 = f1 = f2 = matrix(rep(0, length(p1)*length(p2)), nrow=length(p1))
  for(i in 1:length(p1)) for(j in 1:length(p2)) {
    s1= u1 - p1[i]; s2 = u2 - p2[j]
    q1[i,j] = sum( s1 > 0 & s1 >= s2 )
    q2[i,j] = sum( s2 > 0 & s1 <  s2 )
    f1[i,j] = (p1[i]-mc1) * q1[i,j]
    f2[i,j] = (p2[j]-mc2) * q2[i,j]
    f0 = f1  + f2 }
  m0 = max(f0); w0 = which(f0 == max(f0), arr.ind = T)
  p1s = p1[w0[1]]; p2s = p2[w0[2]]
  par(mfcol=c(1,1),mar=c(5,5,3,4))
  filled.contour(p1, p2, f0, color=terrain.colors, nlevels=8,
    plot.title=title(cex.main=1,family="serif",font=4,
      main=sprintf("Aggregate Profit over Price Space\n( %s + %s )",
                   paste0(pd1,collapse=""),paste0(pd2,collapse="") ),
      xlab=TeX("$p_1^*$ (given.  $p_2$)"),
      ylab=TeX("$p_2^*$ (given.  $p_1$)")),
    key.title=title(main="\nTotal Profit",cex.main=0.8),
    key.axes=axis(4, cex.axis=0.8),
    plot.axes={
      axis(1, cex.axis=0.8); axis(2, cex.axis=0.8)
      lines(p1[apply(f1,2,which.max)],p2,col=clr[1],lwd=2)
      lines(p1,p2[apply(f2,1,which.max)],col=clr[2],lwd=2)
      text(8.5,12,TeX(sprintf("$\\pi^*(%.1f,%.1f)=%.1f$",p1s,p2s,max(f0))),pos=1)
      points(p1s,p2s,pch=19)
    })
}

pSpace(c(1,2,3,1),seq(4,12,0.1),c(3,2,3,1),seq(4,12,0.1))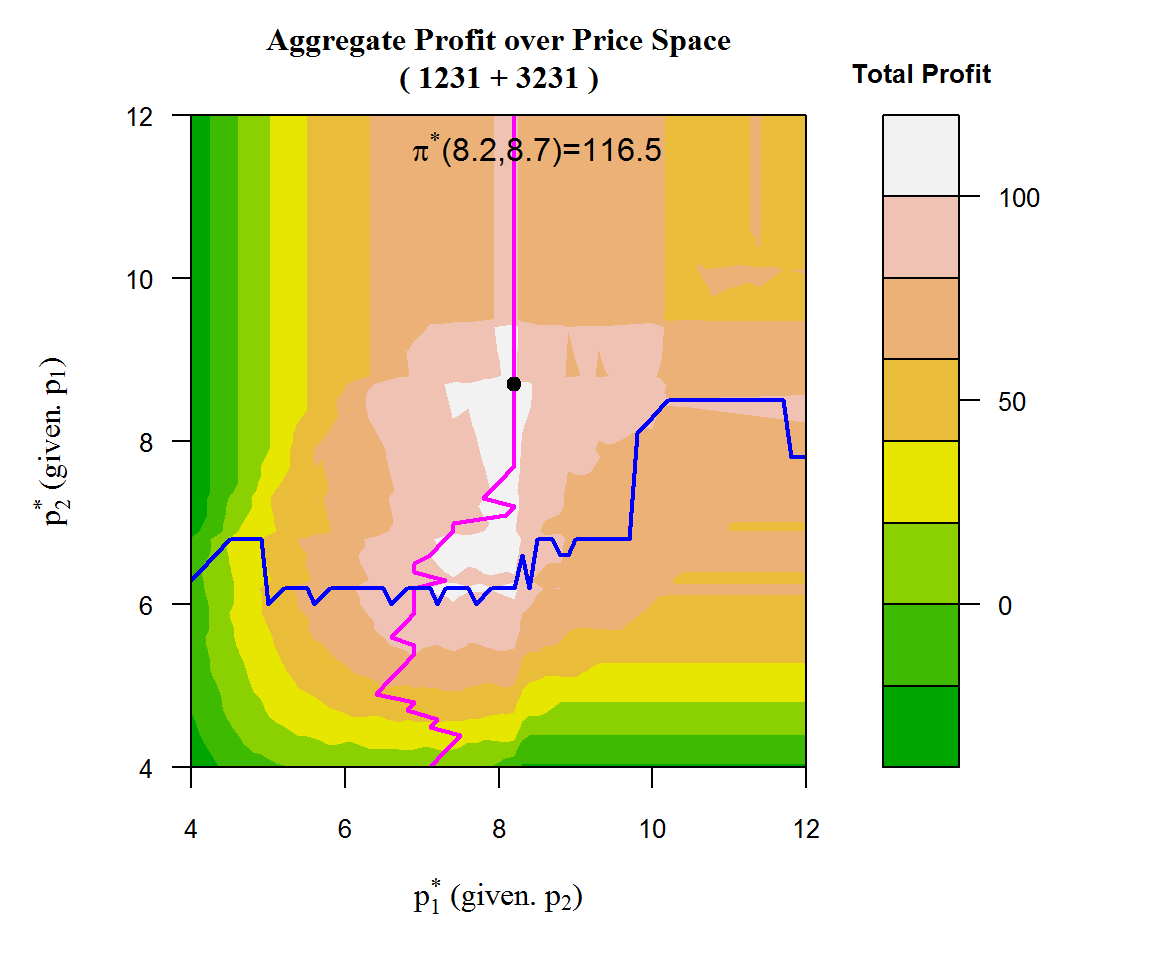

根據上圖：如果這兩個產品相互競爭，結果會是？
那如果這兩個產品屬於同一家公司呢？

4.4.2 產品組合

在這個例子裏面，總共有有多少可能的雙產品組合呢？

(3*3*3*2)*(3*3*3*2-1)/2

## [1] 1431

想要把所有產品組合掃過一遍，需要花一點時間。

source('scan.R')

4.4.3 模擬結果

我們把模擬的結果之中，每一個產品組合的最佳的營收和獲利畫出來：

load('df.Rdata')
hchart(df,"scatter", hcaes(x=revenue,y=profit,group=opt,lab,p1,p2,q),radius=3) %>%
  hc_plotOptions(series=list(allowPointSelect=T)) %>%
  hc_chart(zoomType = "xy") %>% hc_add_theme(hc_theme_flat()) %>%
  hc_tooltip(headerFormat = "",valueDecimals=1,borderWidth=2,
    hideDelay=100,useHTML=T,padding=3,
    pointFormat="<center>{point.lab}</center> Price: {point.p1},{point.p2}<br>
                 Q'ty: {point.q}<br> Rev.: {point.x}<br> Profit: {point.y}") %>%
  hc_colors(hex_to_rgba(c('darkgreen','orange'), alpha = 0.5)) %>%
  hc_legend(floating=T,align='left',verticalAlign='bottom')

上圖裡面，有多少個策略是合理的呢？
看到市場模擬的結果之後，你會想要調整你的策略目標嗎？如何調整？

4.5 產品差異的重要性

我們把獲利最大的產品組合的獲利函數畫在價格平面上面：

pSpace(c(1,2,3,1),seq(4,12,0.1),c(3,3,3,2),seq(4,12,0.1))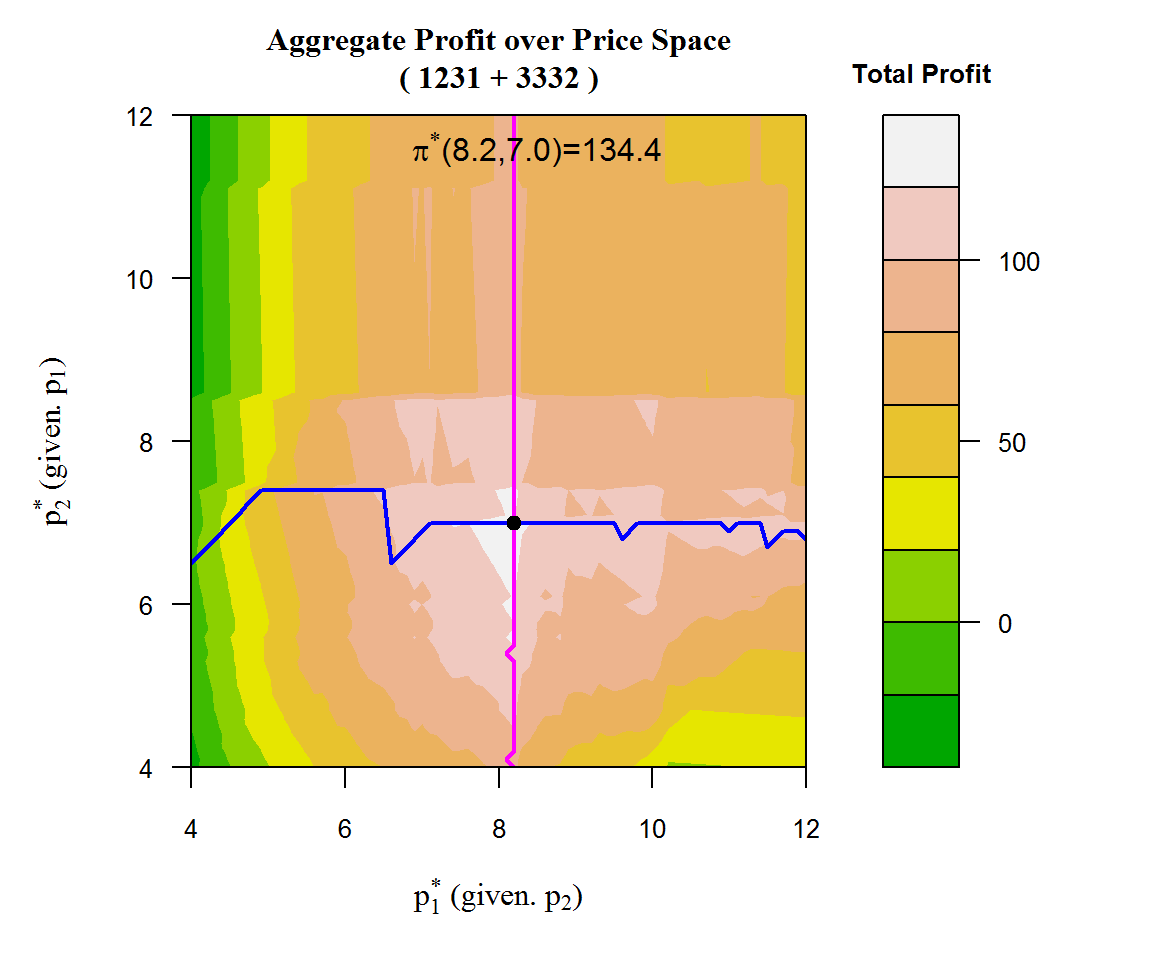

在上面最佳的產品組合裡面，競爭和合作的均衡正好是相同的，這種現象代表什麼？它的策略意涵是？

Wrap Up - Competition & Differentiation

兩種策略：產品線規劃、競爭策略
兩種競爭形式：內部競爭、外部競爭
兩種競爭方法：價格競爭、差異化
無差異的產品競爭：獲利來自於生產成本的差異
差異小：策略(價格)互補、削價競爭
差異大：策略(價格)獨立、壟斷價格